我是一颗树,之前我们数据结构家族中的一个小朋友——“栈” 已经给你们介绍过的我们这个家族了(我是一个“栈”)。之所以叫栈为小朋友,是因为我和他的爸爸——数组是平辈的。
之所以存在我们这样一个家庭,最主要的原因是数组他们家庭虽然很强大,但是有一定的局限性。大家都知道,无论是数组、链表以及他们家的那几个小娃娃(栈、队列)等,存储的数据之间都只有简单的前后顺序关系。
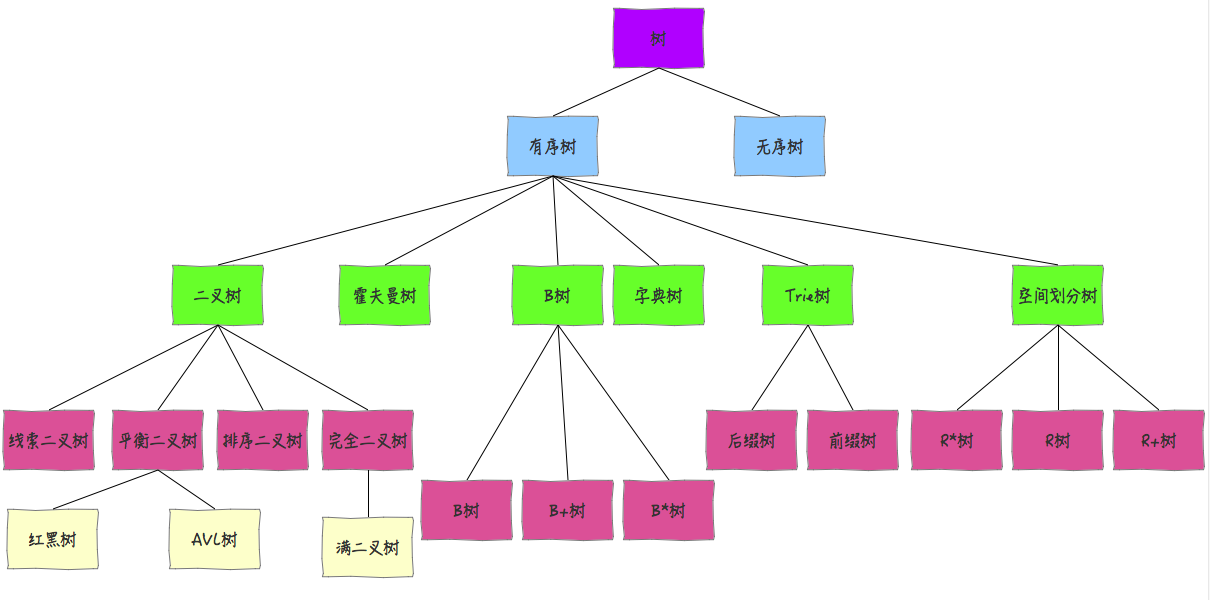
既然说到这了,那就在给你们科普一下整个数据结构大家族吧。毕竟你们认识的那个“栈”只是个小晚辈,对我们家族的历史什么的都不是很了解。
数据结构,主要有两个作用,第一个是存储数据,第二个是可以反应所存储的数据之间的逻辑关系,注意,逻辑关系并不是他们在计算机中存储的物理位置关系哦。所以,根据大家存储的数据的逻辑结构的不同,主要可以分为这个几个大的分支:
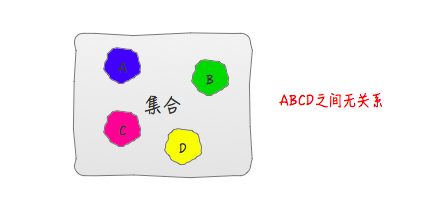
- 集合
- 他们家帮别人存储的数据之间什么关系都没有,唯一的关系可能就是同处于同一个集合了。
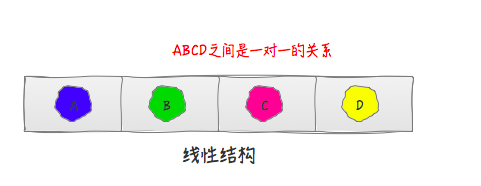
- 线性结构
- 他们家呢,帮别人存储的数据之间是有顺序的,数据之间在逻辑上是首尾相接的连续保存的。所以,元素之间存在着一对一的关系。比如你们认识的数组家族,就是线性结构的。
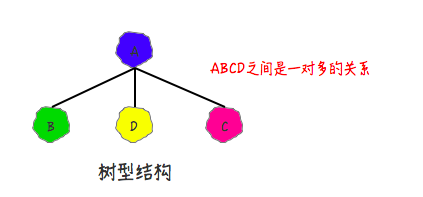
- 树形结构
- 嘿,这就是我们的家族啦,我们存储元素存在着一对多的相互关系。
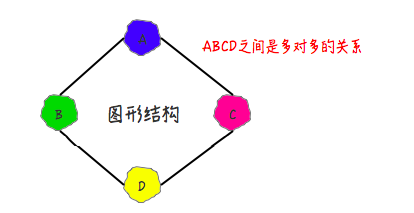
- 图形结构
- 图形结构分支是一种复杂的数据结构。数据元素间的关系是任意的。任意两个数据元素间均可相关联。
大家了解的数组、队列、栈、链表他们都属于线性结构的分支的。今天的主角,也就是我和我的“树”家族是树形结构这个大的分支中的。
也许你已经猜到了,我是整个数据结构大家族的树形结构这一分支的族长。作为一个庞大的家族分支,我们当然具备整个数据结构家族的基本功能——数据存储。另外,整个树形分支主要用来保存具有树形结构的数据集合。说的白一点,就是我们帮别人存储的数据是有层次关系的。就像自然界中的一颗倒置的树一样。
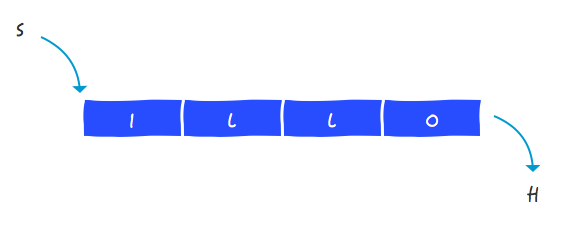
先来说下找我们保存数据的一些限制和要求吧。我们帮别人保存的每个元素我们称之为节点,而我们一般有一个特定的结点被称为根节点,其余的结点都叫非根节点。下面给你看一颗标准的树,然后通过这张图,再来介绍下什么是叶节点、父节点等概念。
H节点是O和L的父节点,O和L是H节点的子节点。 H节点是根节点,因为他没有父节点。 I、S和L节点是叶结点,因为他们没有子节点。 I和S是兄弟节点,因为他们的父节点都是O节点。
好了,说好了这些了,该带你见一见我的家族成员了。作为数据结构的树家族的大家族,我有很多后代。先来给你看下我的家谱:
我有两个儿子:小儿子有序树、大儿子无序树。大儿子是家族的顶梁柱,承担起了家族的很多工作。而我的小儿子,就是一个比较自由的孩子,无忧无虑的什么也不管,所以大家有时候也叫他自由树。
先来说说这个我十分宠爱的小儿子——无序树。
无序树
无序树,他也是个树形结构,除了树中的父子节点之间有关系以外,同一个父节点的所有子节点之间是没关系的,在树中,这种关系就是顺序,比如谁在前谁在后。所以,他叫无序树。另外,我的这个小儿子由于太过自由,至今都没给我生出个娃娃来。所以,我的小儿子是个孤家寡人。
再来详细说说他的数据存储方面的事情,前面说了,他存储的数据之间只有父子节点间有关系。如果你让他帮你存储A、B、C三个数据的话,1个父节点,2个子结点的情况有 3 种。
无论两个子节点位置关系如何,都是同一棵树。即A-B-C和A-C-B被认为是同一棵树。
有序树
再来介绍一下我的大儿子,整个树家的顺位继承人。他真的做到了一个长子应该做的所有事情,他和他的孩子们几乎包揽了树家族的所有工作内容。
他和无序树的区别比较明显,就是在有序数中,子节点之间是有顺序关系的。如果你让我的大儿子帮你存储A、B、C三个数据的话,1个父节点,2个子结点的情况有 6 种。
只要两个节点的顺序掉换一下,又是一个新的树。A-B-C和A-C-B被认为是两棵不同的树。
从上面的家族图谱中可以发现,我的大儿子有序树也有很多孩子的。其中我比较出名的三个孙子分别是二叉树、霍夫曼树和B树等。
现在的年轻人,都很有个性的,帮别人存储数据的时候都有很多要求呢,不过也好,年轻人嘛,就应该有点性格。也得益于他们的各自的特性,树家族才能如此强大。
关于有序树的几个晚辈的介绍,后面让他们自己来吧,我这把老骨头说了这么多也累了。







小儿子有序树,大儿子有无序树,后面说:来说说小儿子有无序树,这里是不是写歪了